Micro-annulus repair

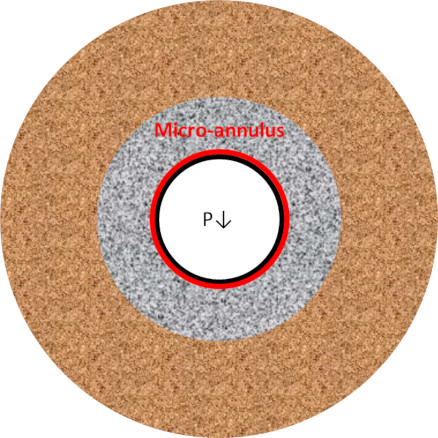
Before initiating a squeeze treatment to plug a micro-annulus between the cement sheath and either the casing or formation, it is worth considering what volumes, rates and pressures should be expected from the process, if the sealing fluid is correctly placed into the micro-annulus. 

The following is an estimation of the expected values of the treatment parameters based on idealised situations.  Although there is a high uncertainty in many of the variables involved the analysis shows the order of magnitude of the expected values.

Assumptions

I have made the following general assumptions in the analysis.  A 7-inch casing has been used for the calculations.

The micro-annulus has a uniform width (w) circumferentially and longitudinally. 

The injection fluid is Newtonian with a low viscosity (𝜂).  Fluid viscosities of 1, 5 and 10 mPa.s are used in the examples.

The properties of the fluid remain constant; there is no reaction or filtration of the fluid.

The micro-annulus is gas filled before the injection of the fluid so there is no significant pressure drop associated with displacement of the gas.

All the above assumptions are likely to lead to an underestimation of injection pressures and an overestimation of injection rates compared with real situations.

Volume of a micro-annulus

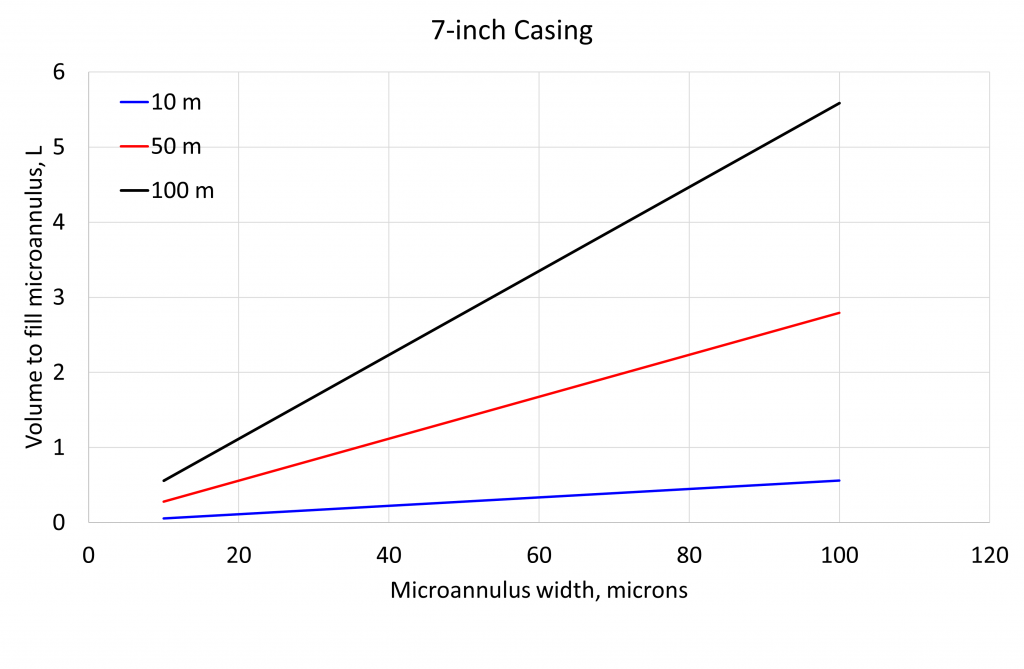
The volume of fluid to plug micro-annuli are surprisingly small.  The following graph shows the volume of a fluid required to plug a given length (10, 50 or 100 m) of a micro-annulus of a given width (from 10 to 100 μm).  Even for a wide (100 μm) micro-annulus less than 6 litres of fluid is required to fill it along a length of 100 m.

Constant injection rate

Low-rate injection techniques to repair micro-annuli were proposed twenty years ago by Slater, Stiles and Chmilowski (SPE 67775).  They used injection rates of 10 L/min and lower to inject micro-cement slurries into micro-annuli.

The pressure drop required to inject a Newtonian fluid through a micro-annulus as a function of rate can be calculated using standard equations, for example those given in Appendix A of Well Cementing, 2^nd Edition. 

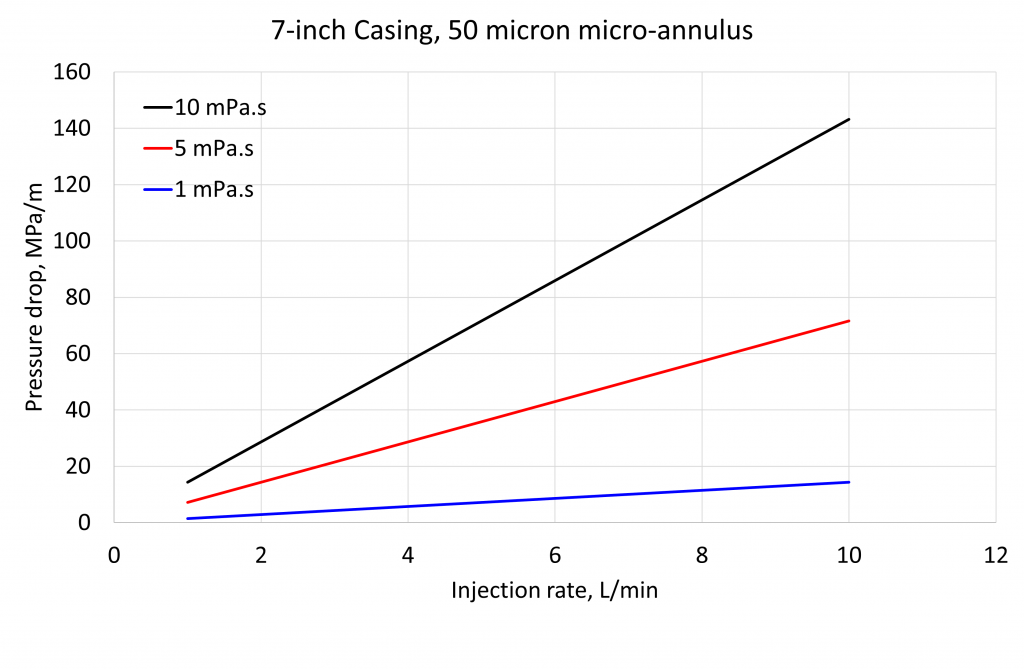
The results are shown below.  For water (viscosity = 1 mPa.s) the pressure drop is 14.3 MPa/m (630 psi/ft) at 10 L/min and 1.4 MPa/m (63 psi/ft) at 1 L/min.  The pressure drop increases linearly with increasing flow rate and increasing fluid viscosity (3 examples given).

Even with some of the lowest viscosity sealants available, such as D264 Nanosealant, injection rates will be low with typical injection pressures.

Constant injection pressure

For hesitation squeezes the time for the fluid to travel a given distance in a micro-annulus at a constant injection pressure can also be calculated.  The figure below shows the time taken for sealant fluids of two different viscosities (5 and 10 mPa.s) to fill a given depth of micro-annuli (50 and 100 μm wide) at a constant injection pressure of 6.9 MPa (1000 psi).  The effect of the micro-annulus width is greater than that of the fluid viscosity.  The penetration depth, and hence injection rate, is proportional to w³ and inversely proportional to 𝜂.

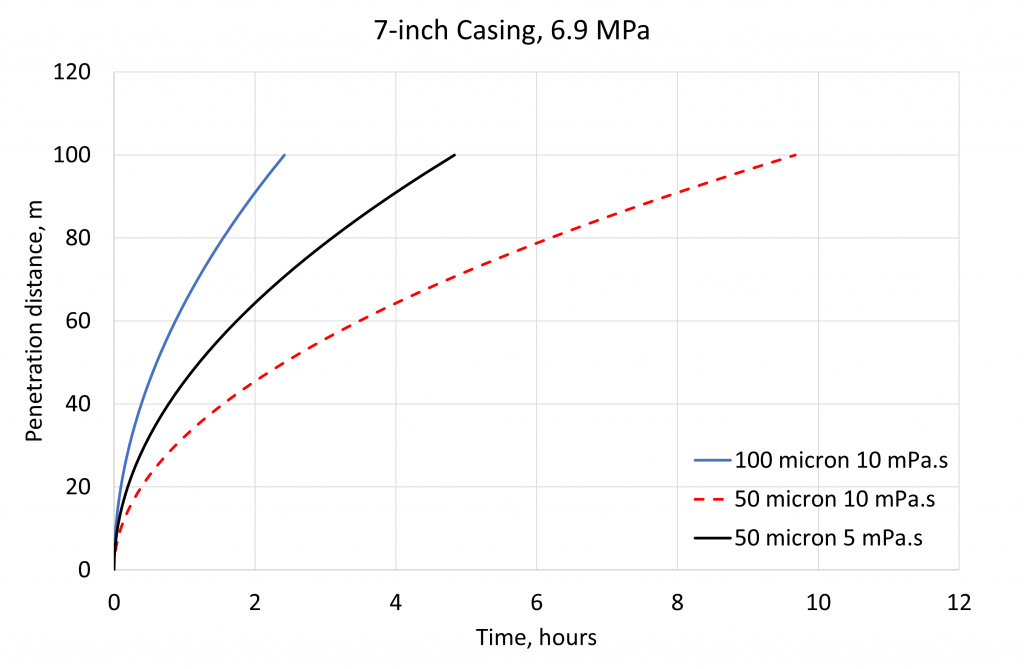
The average flow rate into the micro-annulus can also be calculated as a function of the depth of micro-annulus filled.  The average flow rates into the micro-annulus as a function of depth filled are given in the table below.  The average flow rate is calculated over time periods corresponding to filling the first 1 m, filling from 10 m to 11 m and for filling from 95 to 100 m.  Decreasing the width by a factor 2 decreases the flow rate by a factor 8, while decreasing the viscosity by a factor 2 doubles the injection rate.

Penetration depth	100 μm, 10 mPa.s	50 μm, 10 mPa.s	50 μm, 5 mPa.s
0 to 1 m	7700	960	1920
10 to 11 m	368	46	92
95 to 100 m	39.5	4.9	9.8

Volume injected from pressure decay

The pressure decay in a hesitation squeeze treatment is a function of the compressibility of the fluid, the volume of fluid pressurised (including the entire volume contained in the coiled tubing or drill pipe) and the volume of fluid that flows into the micro-annulus (assuming that there are no leaks or flow paths).

As an example, consider 5 m³ of water pressurised to 6.89 MPa (1000 psi) with the pressure then decreasing to 6.21 MPa (900 psi).  The compressibility of water changes with temperature and pressure (Fine and Millero, 1973).  In this example at 20°C and 6.9 MPa we can take a value of 4.5 x10^-10 Pa^-1.  For a pressure drop of 0.689 MPa (100 psi) in 5 m³ the volume change is 1.5 L.  Given the volume flow rates calculated above after the initial penetration into the micro-annulus, the pressure decay of 100 psi will occur over periods of hours to tens of hours.

Summary

The calculations above are order of magnitude estimations on what to expect when squeezing micro-annuli.  Squeeze volumes are small (litres not m³), injection rates will be low and squeeze pressures high.  For hesitation squeeze treatments pressure decreases will occur over hours.  If one or more of these parameters are significantly different then it is likely that other flow paths are present.